When is a reverb not a reverb? When it's a filter, of course! There's more to convolution than meets the ear, and creative processing of impulse responses can yield extraordinary results.
The common perception of convolution reverb plug‑ins, which are based on the use of impulse responses, is that they offer great realism, but limited potential for experimentation. In this article, however, we'll be exploring the creative side of convolution. Being audio files, impulse responses can be edited, modified and even created from scratch, and we'll see how this opens up new ways of processing sound. I'll be proposing several innovative methods for impulse response authoring and processing, and offering an original understanding of reverberation.
This article is accompanied by a number of audio examples, which are available on‑line at /sos/sep10/articles/convolutionaudio.htm. The audio examples are all numbered, so I'll refer to them simply by their number in the text. Most reverberation examples are based on a single dry audio file that was recorded inside an anechoic chamber (see audio example 1). I have also provided a number of impulse response files corresponding to the relevant audio examples, as 24‑bit, 44.1kHz WAV files.
The Spirit(s) Of Reverberation
Impulse response convolution is best known as a technique for adding reverberation to a given sound in a realistic way. That said, realism in terms of reverberation is not always an easy concept to define, reverberation being a complex and multi‑faceted phenomenon. St. Peter's Basilica produces reverberation, and so does your shoe cupboard: two transformations that have little to do with each other from a perceptual point of view, though they both qualify as reverberation.
Moreover, when we're using reverberation in a mix, realism isn't necessarily required, nor is it always welcome. Certainly, reverberation can be used to give recorded music a sense of being performed in a real acoustic location; but it can also be used to provide an acoustic environment to a given track so it stands apart from the mix. In this case, realism in the reverberation can be welcome, but it's not the main purpose. Going further, one can add reverberation purely for sound‑design purposes, in which case realism is not an issue.
As we can see, there are many points of view from which to consider reverberation. In this article, we'll forget about realism, and remain open to the idea that an impulse response (or IR for short) recorded from a cardboard tube and then processed digitally using EQs or any other audio tool provides as interesting a timbre as one recorded realistically from Vienna's Musikverein venue. We will study impulse responses and convolution plug‑ins for their ability to transform sound and create particular timbres. Convolution reverbs provide a convenient way to extend the notion of reverberation to new limits, and discover sounds that were previously unheard — and that's what we're after here.
What's Possible With Convolution
To master the process of impulse response convolution, it's important to be aware both of what it can do and what it can't do. Impulse responses are audio files that contain information about audio transformations. They're designed to be used in convolution engines that know how to interpret this information. These can be of two kinds: reverberators and filters. It's very important to understand that impulse responses are not able to capture anything else. They're just not the right tool to capture compression, distortion, pitch‑shifting or modulation effects. For instance, trying to generate an impulse response from a Manley Variable Mu compressor just doesn't make any sense. This unit's interest lies in the compression's attack and release shapes, as well as in the fantastic colour of the harmonic distortion it generates when pushed hard. Neither of these features can be captured inside an impulse response file.
To get a better understanding of the issue, it may be useful to consider to what extent an impulse response is able to capture the sonic characteristics of a hardware EQ — not a theoretical filter, but an actual analogue outboard EQ, which does much more than frequency filtering. Making an IR from such a unit can make sense, but it will leave out a number of the unit's intrinsic properties, such as harmonic distortion, background noise and dynamic behaviour. This would be particularly true of a budget tube EQ such as the Aphex 109. This sometimes generates quite a lot of what seems to be intermodulation distortion, softening the sound considerably and making the unit unique, in a nice way. When taking the impulse response of a 109, you can forget about the uniqueness: what you will get is a plain, digital filter. Not really an EQ, just a filter. It's not the same.
Never forget that impulse response‑based processing is, in essence, digital. What's more, it's strictly deterministic. If you play a given sound inside a convolution plug‑in, you will always get exactly the same result. This would not be true in the case of acoustic situations such as reverberation from real rooms, in which you never get the exact same response twice, no matter what.
Reverberation Basics
Before actually dealing with convolution reverbs, let's take a closer look at reverberation itself. Acoustic reverberation can be divided into two stages: first or early reflections, and the diffuse field that comes after these. Early reflections are easy to understand: imagine that you're at your desk, in front of your laptop. Reading this article, you may very well be in this precise situation. If you speak, the sound of your voice will strike your computer screen and keyboard, and bounce back to you directly. These reflections are discrete, as opposed to continuous: they can be identified individually. In an impulse response file, they appear as peaks, or clicks.
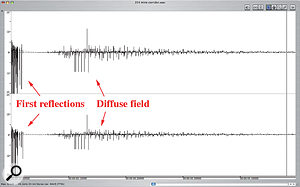 This preset from the TC Electronic M3000 shows a clear distinction between early reflections and diffuse field.The diffuse field is less easy to understand. Imagine you're shouting in a big factory. The sound of your voice will strike the surfaces around you, creating the first reflections. In turn, these reflections will be reflected and diffracted on other surfaces, creating other reflections, which will also be reflected… and so on. Eventually there will be so many reflections that the resulting sound will become continuous. This continuous stream of reflections makes the diffuse field. In an impulse response file, the diffuse field appears as a continuous noise.
This preset from the TC Electronic M3000 shows a clear distinction between early reflections and diffuse field.The diffuse field is less easy to understand. Imagine you're shouting in a big factory. The sound of your voice will strike the surfaces around you, creating the first reflections. In turn, these reflections will be reflected and diffracted on other surfaces, creating other reflections, which will also be reflected… and so on. Eventually there will be so many reflections that the resulting sound will become continuous. This continuous stream of reflections makes the diffuse field. In an impulse response file, the diffuse field appears as a continuous noise.
 A different preset from the same unit, by contrast, shows a gradual transition between early reflections and diffuse field.In actual rooms, discrete early reflections gradually become too numerous to be discriminated individually, thus turning into a continuous diffuse field. There is no clear limit between one and the other. However, the distinction is useful to make, in order to understand how reverberation works. Also, some non‑convolution‑based digital reverb algorithms use separate processes to generate early reflections and the diffuse field, with no gradual transition from one to the other. If you take an impulse response from such an algorithmic reverb, the two are clearly distinct. For instance, the impulse response whose waveform is shown right was recorded from the TC Electronic M3000 using preset 354, 'Mine Corridor'. There is no smooth transition between early reflections and diffuse field. Both can be clearly distinguished.
A different preset from the same unit, by contrast, shows a gradual transition between early reflections and diffuse field.In actual rooms, discrete early reflections gradually become too numerous to be discriminated individually, thus turning into a continuous diffuse field. There is no clear limit between one and the other. However, the distinction is useful to make, in order to understand how reverberation works. Also, some non‑convolution‑based digital reverb algorithms use separate processes to generate early reflections and the diffuse field, with no gradual transition from one to the other. If you take an impulse response from such an algorithmic reverb, the two are clearly distinct. For instance, the impulse response whose waveform is shown right was recorded from the TC Electronic M3000 using preset 354, 'Mine Corridor'. There is no smooth transition between early reflections and diffuse field. Both can be clearly distinguished.
The second impulse response was recorded from the same unit, this time using preset 305, 'Wide Garage'. By contrast with the first example, early reflections are gradually turned into diffuse field, and it's difficult to distinguish a clear point at which this happens.
 Diffuse field in the impulse response from a bedroom closet.Intuitively, one would think that only large spaces, such as cathedrals, produce a diffuse field. Indeed, if you clap your hands in your bedroom, it's unlikely that you will actually hear a clear diffuse field, such as the one you can hear in a warehouse. But in truth, in any acoustic space, there is always a diffuse field. It's just that in small spaces the reverberation is too short, everything happens too quickly, and it's impossible for the ear and the brain to discriminate the early reflections from the diffuse field. For instance, consider the impulse response whose waveform is shown on the right, recorded from a bedroom closet. This is indeed diffuse field! No early reflections are apparent. Refer to audio example 2 to hear the result of such an IR, and to obtain the corresponding IR file.
Diffuse field in the impulse response from a bedroom closet.Intuitively, one would think that only large spaces, such as cathedrals, produce a diffuse field. Indeed, if you clap your hands in your bedroom, it's unlikely that you will actually hear a clear diffuse field, such as the one you can hear in a warehouse. But in truth, in any acoustic space, there is always a diffuse field. It's just that in small spaces the reverberation is too short, everything happens too quickly, and it's impossible for the ear and the brain to discriminate the early reflections from the diffuse field. For instance, consider the impulse response whose waveform is shown on the right, recorded from a bedroom closet. This is indeed diffuse field! No early reflections are apparent. Refer to audio example 2 to hear the result of such an IR, and to obtain the corresponding IR file.
Discrete Or Diffuse?
To get a better understanding of the transition between discrete reflections and diffuse field, it can be useful to carry out a simple experiment. For this purpose, let's consider a derivative of what's called a Dirac Impulse: a short impulse, which can be digitally rendered as a single '1' in a series of '0's. The screenshot shows such a waveform in BIAS Peak.
 A Dirac Impulse in BIAS Peak.Considered as an impulse response, this Dirac Impulse corresponds to a single delay, which does not colour the sound at all. For those versed in mathematics, this Dirac Impulse is the 'identity element' of convolution, and as a consequence, of impulse responses. Now, if we add four other Dirac Impulses to this first one, we will get an IR with five reflections, corresponding to five discrete echoes. The more Dirac Impulses we have in an impulse response, the more reflections we get. Let's continue adding Dirac Impulses to each other in a random way, until eventually we end up with an impulse response that contains 32,000 reflections. An interesting phenomenon will then happen: above a certain number of reflections, the ear will not be able to discriminate between the reflections, and will begin to hear a diffuse field.
A Dirac Impulse in BIAS Peak.Considered as an impulse response, this Dirac Impulse corresponds to a single delay, which does not colour the sound at all. For those versed in mathematics, this Dirac Impulse is the 'identity element' of convolution, and as a consequence, of impulse responses. Now, if we add four other Dirac Impulses to this first one, we will get an IR with five reflections, corresponding to five discrete echoes. The more Dirac Impulses we have in an impulse response, the more reflections we get. Let's continue adding Dirac Impulses to each other in a random way, until eventually we end up with an impulse response that contains 32,000 reflections. An interesting phenomenon will then happen: above a certain number of reflections, the ear will not be able to discriminate between the reflections, and will begin to hear a diffuse field.
Refer to audio examples 3-15 to hear the transition from discrete reflections to diffuse field. Example 3 is based on five Dirac Impulses within a one‑second timeframe, example 4 on 10 Dirac Impulses, and so on up to example 15, which is based on 32,000 Dirac Impulses. The corresponding IR files are also provided. If you listen to the IR files themselves, you'll hear that discrete Dirac Impulses seem to completely disappear when there are more than 4000 of them. When listening to the audio examples, a diffuse field begins to be heard above 500 simultaneous Dirac Impulses.
The Difference Between Reverberation And Filtering
Let's consider the perceptual disappearance of the discrete reflections and the advent of the diffuse field in the example above. This phenomenon happens at between 200 and 500 discrete Dirac Impulses in a one‑second span. This would suggest that the human ear is able to discriminate phenomena that are separated by a period of 50ms, but not by a period of 20ms. Consequently, it means that there is a time constant above which the ear is capable of discriminating consecutive events, and below which it is not.
This constant does indeed exist: it's called the ear's integration time. It's a very important notion as far as hearing is concerned. To make this notion perfectly clear, consider two extremely short audio samples, such as digital clicks. If those two clicks are played back with a one‑second interval between them, they can easily be discriminated. Play those clicks with a 100ms interval between them and it's still possible to hear two clicks, but it's less easy. Play those two clicks a mere 10ms apart and it's impossible to hear two clicks: they are perceptually merged with each other. In place of the two clicks, we hear one compound sound. The time interval over which those two clicks can be discriminated is called the ear's integration time, and is described in the technical literature as around 40 to 50 milliseconds.
This is a very important phenomenon. It is what makes us able to hear pitch instead of consecutive sound events: 50ms corresponds to a frequency of 20Hz, which is the lower range of human audition. In the context of reverberation, it is what turns discrete reflections into diffuse field. It also brings another interesting consequence. Consider an impulse response around 100ms long: perceptually, this impulse response corresponds to a reverb. Then, consider an impulse response that is only 10ms long. This impulse response is not perceived as a reverb — as something that possesses an existence over time — but as a filter, something that is perceived as being instantaneous.
Quite importantly, this means that as far as impulse responses are concerned, reverbs and filters are the same thing, based on the same content. Only perception makes them different. In this article, it means that by dealing with convolutions in general, we'll deal with both reverberation and filtering.
The Continuum Between Reverb And Filtering
Now that we know that the only difference between reverb and filtering is the span of time over which the phenomenon happens, we're going to convert a reverb into a filter, by gradually reducing the length of its impulse response.
For that, I've used the Change Duration function in BIAS Peak, but we could have used any other time‑stretching algorithm. We start with the impulse response recorded from a small indoor pool. It lasts about two seconds, and features a clear‑sounding reverb, with harmonic normal modes developing near the reverb tail. We process this impulse response repeatedly, each time reducing its duration by 50 percent. After five or six passes, the impulse response loses its reverb aspect. At this point, its duration is respectively circa 60ms or 30ms. After 11 passes, its duration is 1ms, and it's definitely a filter, with a frequency response that seems to correspond with the averaging of the initial reverb's frequency response over time.
The audio examples corresponding to this experiment, along with the corresponding IRs, are numbered 16 to 27. Listen through them in sequence and you'll hear how the room sound seems to shrink, eventually turning into a filter that keeps some characteristics of the initial room.
This is an interesting experiment, but it also provides an interesting range of unusual impulse responses that can be of great use in production: a variety of small spaces, along with interesting filters that would be hard to get on an actual EQ.
Let's try that again, this time starting with a completely synthetic IR, processed from a pseudo‑periodic oscillator. This IR and others like it can be downloaded from http://1‑1‑1‑1.net/pages/impulses/index.htm#lorenz195225. The same phenomenon happens: the reverb gradually turns into a filter, which retains some characteristics of the original IR. Refer to audio examples 28 to 39 to hear the result and get the corresponding IRs.
Let's point out that this method is more empirical than scientific. If we had used another time‑stretch algorithm, we would have obtained slightly different results. On a practical note, be warned that very short IRs can't be used with Audio Ease's Altiverb 6. This is apparently a software limitation, because there are no problems with Space Designer in Logic, for example.
Other Ways To Modify IR Length
The examples above show that it's possible to reduce IR lengths with time‑stretching. Another way to do that is to use reverb-time modifying controls built into convolution plug‑ins. Let's begin with Altiverb 6, which has two time‑related controls labelled Reverb Time and Room Size.
The latter is the control that corresponds to what we were doing manually, time‑stretching the IR itself. It's supposed to do a better job than a standard time‑stretching algorithm, since it uses an IR‑specific algorithm. However, it can't provide any drastic IR transformation, being limited to a 50‑200 percent stretch ratio. That makes reverb‑to‑filter conversion impossible.
By contrast, Reverb Time doesn't modify the IR itself, but applies an envelope that either fades it out before the end, or loops the end of the IR and raises its level, depending on whether you want a shorter or longer reverb.
Equivalent controls can be found in other convolution plug‑ins. In Waves' IR1 plug‑in, for instance, the Reverb Time control does the same as in Altiverb 6. In Logic's Space Designer, the Length parameter at the left side of the IR waveform has the same purpose.
 Waves' IR1 provides both static EQ and dynamic damping.
Waves' IR1 provides both static EQ and dynamic damping.
IR Length: Altiverb Vs Peak
Interestingly, the controls built into these convolution reverbs have noticeably different effects from Peak's time‑stretching. Let's start with the small indoor pool IR we've been using to illustrate the continuum between reverb and filtering. Refer to audio example 40 to listen to it.
Now, let's compare Altiverb 6's Time control, set to 50 percent (audio example 41), with the 50 percent time‑stretch in BIAS Peak (audio example 42). Results are comparable, though Altiverb seems to have removed some low‑mid frequencies.
Let's now put Altiverb's Time control to 20 percent (audio example 43), and compare it to the 25 percent time‑stretch we've been using before (audio example 44). Altiverb's algorithm provides a much clearer sound, while Peak's time‑stretch sounds closer to the original reverb.
With its Time control set to 1 percent (audio example 45), it appears that Altiverb doesn't actually reduce the IR length to 1 percent of its original state: it's more comparable with a 12.5 percent time‑stretch in Peak (audio example 46). Using Peak's time‑stretch, the walls are perceptually much more present, and the overall result is much more realistic, and much more reminiscent of the original IR. On the other hand, Altiverb gives a much clearer result, which sounds like what one would normally expect from a reverb in a mix situation. Preference may just be a matter of taste. In any case, we're not going to be able to produce filters from reverbs using Altiverb's Time control: it's not drastic enough.
Let's try the other way around, and set Altiverb's Time control to 150 percent (audio example 47). This time, Altiverb gives a realistic result: it's just like the original IR, only longer.
Let's now switch to Altiverb's Size control. At 50 percent (audio example 48), the result is very strange, in the sense that the reverb really sounds 'medium'. This perceptual aspect is so strong it overrides all others. Plus, it definitely doesn't sound like the original IR. At this ratio, the Time control appears to be preferable, as does the use of Peak's time‑stretch algorithm.
At 150 percent, by contrast, the Size parameter is much more convincing than when set to 50 percent. Compared to the equivalent setting of the Time control, it's more musical (thanks to the attenuation of the hiss), but less realistic.
As a conclusion,what's highlighted is that those controls should be used with caution. They really modify the original IR's timbre, and don't stop at manipulating time aspects, as they're supposed to do. Use of an external time‑stretch algorithm such as Peak's may be preferable for reducing the IR's duration.
 Altiverb 6's Reverb Size and Time controls give surprisingly different results from time‑stretching an impulse response in a third‑party editor.
Altiverb 6's Reverb Size and Time controls give surprisingly different results from time‑stretching an impulse response in a third‑party editor.
Diffuse Field Authoring With Noise
As we've seen before, a diffuse field is of a continuous and noisy nature. Indeed, any audio content that's continuous and noisy can provide a base for a diffuse field, including white noise. Let's generate white noise with HairerSoft's Amadeus or any program that can do it. Then, let's fade it out — a reverb usually fades out with time — and use the resulting audio file as an IR. As heard in audio example 50, it sounds like a very clear, acoustically untreated space. We can do the same experiment with pink noise (audio example 51): it also sounds like an acoustically untreated space, albeit made from a different material.
Now we want to improve the diffuse fields that are obtained from white or pink noise. What we can do? Filtering the IR will modify the reverb's colour, but better still, we can filter the IR dynamically. For instance, we can automate the EQ with which we process the IR. Let's consider how to do that in a way that makes sense. In real, acoustic spaces, when a sound wave is reflected from a surface, its spectral colour gets modified. In other words, it gets EQ'd. Now, remember that diffuse field is made from a continuous stream of reflections: since the sound is changed each time it's reflected, it means that the spectral colour of the diffuse field changes continually.
We can suppose that while the colour itself changes over time, its rate of evolution doesn't vary: after all, in an actual acoustic space, the properties of the walls will be constant. This means that we could apply a slight EQ at first, which would get more drastic over time, while keeping the same overall profile. This would reflect the repeated reflections the original sound undergoes as it bounces off the surfaces, in effect being EQ'd multiple times using the same settings. Audio examples 52 to 54 show the kind of results one can expect from such a technique.
Some convolution plug‑ins, such as Waves IR1 or Altiverb 6, include a 'damping' parameter that applies a simplified form of dynamic EQ. Audio examples 55 and 56 show the result of damping in the IR1 plug‑in. The simple dynamic EQ'ing is clearly audible, and in fact, custom dynamic EQ'ing in your DAW can give much better results. Audio examples 57 and 58 show the result of static EQ'ing using equivalent settings, clearly illustrating the difference.
Also keep in mind that it's not necessary to start with faded white or pink noise: other noises can be a good starting point for diffuse-field authoring, such as tape noise, amp buzzes, lightly noisy ambiences, and so on. The only limit is your creativity.
Percussive Samples As IRs
If we look at any given set of impulse responses, we'll find that a vast majority of them feature a decreasing dynamic profile. This seems to be natural enough: if you clap your hands in any given place, the resulting reverberation will not get louder over time. That would be quite absurd. In practice, if you use an impulse response with a dynamic profile that is increasing or even stable, you will find that the result quickly becomes incomprehensible. While reverse and gated reverbs do, respectively, feature increasing and stable dynamic profiles, their use remains quite specific.
This raises a simple question: if I take any short sample with a decreasing dynamic profile, will that make a suitable impulse response? The answer is: that depends. Impulse responses with too much of harmonic content, such as a piano chord, often lead to cheesy results. Responses with too many low frequencies, such as a kick‑drum sample, can lead to completely incomprehensible results. Remember that most reverbs exhibit spectra that are quite smooth, without strong formants, and with quite a lot of high frequencies (canonic models being white and pink noises). When experimenting with impulse responses, those are good models to keep in mind.
Now, there is one kind of instrument that definitely meets these criteria, and that's the cymbal. Cymbal samples, especially short ones, can make interesting impulse responses, perfect for eerie vocals or metallic‑sounding keyboards. They are also useful when you've got way too many tracks to fit into a mix, but for some reason you can't mute any of them (maybe because the other musicians or the producer don't want you to). In this situation, it's necessary to decrease the 'timbral largeness' of those tracks in one way or another. Lo‑fi plug‑ins and filters can help: so, too, can convolution with short cymbal samples, in combination with EQ'ing. Audio examples 59 and 60 are two illustrations of cymbals used as impulse responses.
Speakers & Headphones As IRs
Speakers and headphones naturally change the timbre of any sound that's played through them, and sometimes add a very soft and small acoustic ambience, depending on when you put the mic while recording the IR. Generally speaking, cheap speakers and headphones tend to generate obvious filtering, while the use of more expensive gear will result in more subtle changes. Such soft EQs can bring interesting results in production, especially when recorded along with the smallest touch of acoustic ambience — which means putting the microphone perhaps 5cm from the speaker, or 2cm from the headphone driver. Used in mixing, they can bring a distinct yet non‑obtrusive acoustic colour to an otherwise dry track. Refer to audio examples 61 to 65 to listen to three speaker IRs and two headphone IRs in action.
Impulse responses obtained from speakers and headphones are also highly reconfigurable, meaning they can easily cascaded or combined together. Audio examples 66 and 67 provide two examples of 'doubled' speaker and headphone IRs. Other solutions can be found, such as creating coloured echoes from speakers, as shown at http://1‑1‑1‑1.net/pages/impulses/index.htm#SpeakerEchoes.
Space Designer Programs
Digital space designers such as Voxengo's Impulse Modeler are great for creating special IRs. For instance, you may want to create absurdly huge or tiny spaces. As demonstrated in audio examples 68 and 69, tiny spaces are particularly interesting for their ability to create highly unusual EQs, with a spectral profile that depends on the simulated surface: cement, gypsum board, glass, and so on.
Once more, if the effect is not obvious enough during production, cascade it with itself, to create "double IRs”, as shown in audio examples 70 and 71. In any case, don't hesitate to experiment with different surfaces, as shown at http://1‑1‑1‑1.net/pages/impulses/index.htm#impulsemod.
Finally, learning a little about MATLAB or similar programs opens up the possibility of synthesizing your own impulse responses from scratch. There's not space to cover this topic in print, but you'll find a guide, with audio examples, at /sos/sep10/articles/matlab.htm.
Conclusion
I hope this article has shown that close study of convolution brings a whole lot of interesting discoveries: reverbs are in fact filters, tiny spaces produce diffuse fields that can be used as an EQ, cymbals can be used as a reverb, and headphones can be used as a processing peripheral. To top it all, during IR recording in location, random mic placements can produce better‑sounding results than academically 'correct' ones (see 'Creative Impulse Response Recording' box, below). Convolution reverbs are open systems, making impulse responses is easy, so don't hesitate: forget about realism and correctness, and be creative!
Creative Impulse Response Recording
A well-known and efficient way to create impulse responses is to record them from acoustic spaces. Many articles exist that explain the process, including a couple in the SOS archives (April 2005, at /sos/apr05/articles/impulse.htm, and February 2008, at /sos/feb08/articles/logictech_0208.htm). However, it is interesting to give some thought to the influence of speaker and microphone placement during IR recording sessions. In concert rooms, it is usual and logical to put the speakers on the stage, and the microphones in a symmetrical setup in front of the stage or in the audience. But when recording the impulse response from a living room, for instance, the issue is not so straightforward, and one can legitimately wonder where to put the speakers and the mics.
The first issue is symmetry: in music production, most reverbs are symmetrical. On the other hand, a living room is seldom symmetrical. This means that when trying to use stereo IRs recorded from domestic spaces in music production, one is almost certain to encounter symmetry issues. This is a problem that can be partially solved during recording by using near‑coincident microphone pairs, such as X/Y setups. This way, the IR will retain some sense of space while being reasonably symmetrical. Alternatively, it's possible to agree with Eric James's opinion in SOS March 2003 (/sos/mar03/articles/stereorecording.asp), and consider that symmetry in reverberation is but an aspect of correctness. This means that if it turns out that the IR is not symmetrical, so be it, and any potential problems that arise during production can be solved during production. This is only reasonable. After all, the main point of a reverb is not to comply with given standards, it's to bring an interesting timbre. Plus, if we need standard reverbs, we don't need to make them ourselves: there are plenty of standard reverbs out there.
Now that we've let aside the symmetry issue, we can get more creative. We can envisage an IR recording session in the following way: with one speaker and one mic, we can record lots of mono impulse responses, with the speaker and especially the microphone being constantly moved around the space. This is not a time‑consuming process: when recording the IR of an acoustic space, what takes time is to bring the gear to the location, and to set it up. Using this method, symmetry issues can be solved afterwards, when recombining those mono‑to‑mono IRs into mono‑to‑stereo or stereo‑to‑stereo ones in post‑production.
Let's illustrate these issues by detailing the recording of the small indoor swimming pool we've been using as an example in this article. This recording was made using two speaker positions and two mic positions, each one featuring a stereo X/Y pair, thus resulting in eight mono‑to‑mono IRs (see audio examples 72 to 79). When combining those mono‑to‑mono IRs into mono‑to‑stereo IRs, we certainly can put together IRs from the same X/Y pair, which would be the 'correct' way to do it. Alternatively, though, it's possible to put together IRs coming from different X/Y pairs, which is definitely not 'correct', for at least two reasons: mono‑to‑stereo IRs created in this way are not symmetrical, and the phase relationship between channels doesn't compare to anything realistic. Correct and incorrect IRs are represented in audio examples 80 to 83, and, in this author's opinion, the 'incorrect' mono‑to‑stereo IRs sound much better than the 'correct' ones.
Generally speaking, unless you're recording IRs inside the Amsterdam Concertgebouw, it's more rewarding to seek something that sounds good than something that's 'correct'. You can also push this principle further and be creative: put mics near walls, under sheets, under seats, in sinks. Experimentation is the whole point of making IRs yourself. Other people, such as the Audio Ease team, are specialists in discerning correctness and do their job perfectly well. Let them deal with this aspect of things.

