It's 70 years since the idea of digital audio sampling was first patented - so it's high time we laid to rest the myths and false perceptions that surround it.
 There's a lot of bollocks spoken and written about digital audio, and some people cling to the idea that it is, in some ineffable and irresolvable way, inferior to analogue audio. But is this true? Does digital audio deserve the reputation it has in some quarters for sounding grainy, brittle and uninvolving? If so, are these epithets a consequence of some fundamental problem, or of poor engineering and implementation? In this article, I hope to answer all of these questions and, in particular, demonstrate why the bad 'rep' that digital audio acquired in the early 1980s is not necessarily appropriate in the 21st century.
There's a lot of bollocks spoken and written about digital audio, and some people cling to the idea that it is, in some ineffable and irresolvable way, inferior to analogue audio. But is this true? Does digital audio deserve the reputation it has in some quarters for sounding grainy, brittle and uninvolving? If so, are these epithets a consequence of some fundamental problem, or of poor engineering and implementation? In this article, I hope to answer all of these questions and, in particular, demonstrate why the bad 'rep' that digital audio acquired in the early 1980s is not necessarily appropriate in the 21st century.
The Birth Of Digital Audio
Pulse-code modulation (PCM) was invented 70 years ago when Alec Reeves, working at ITT (International Telephone and Telegraph), proposed that, rather than represent the changes in air pressure that we hear as audio as a smoothly changing electrical signal (an 'analogue' of the original audio), the voltage could be sampled at regular intervals and stored as a succession of binary numbers (see diagram 1, right). Reeves understood that these samples could only be measured and stored with finite accuracy, but he proposed that the amplitudes of the numerical errors would be less significant than the errors introduced into analogue signals by the electrical noise and low fidelity of the valve equipment of the era.
What Reeves didn't consider (and had no way of testing) was whether these smaller errors would be more or less distracting than the relatively benign hiss introduced by analogue equipment. Nevertheless, the scope of his ideas was impressive, and when he patented them in 1937, he stated that, if no mathematical operations are carried out upon the samples, the quality of digitised and replayed audio depends only upon the quality of the A-D and D-A converters employed. This was, at the time, a radical conclusion, but it has proved to be correct.
 1. The basis of digital audio.Whether he knew it or not, Reeves' ideas were based soundly (no pun intended) on the relatively new mathematics of 'discrete time signal processing', the most important tenet of which is the Sampling Theorem. First proposed as far back as 1915, this states that if a signal contains no frequencies higher than 'B' (the bandwidth) then that signal can be completely determined by a set of regularly spaced samples, provided that the sampling frequency is greater than 2 x 'B'. This means that if you want to sample an audio signal whose highest frequency component lies at 20kHz, any sampling frequency higher than 40kHz is sufficient.
1. The basis of digital audio.Whether he knew it or not, Reeves' ideas were based soundly (no pun intended) on the relatively new mathematics of 'discrete time signal processing', the most important tenet of which is the Sampling Theorem. First proposed as far back as 1915, this states that if a signal contains no frequencies higher than 'B' (the bandwidth) then that signal can be completely determined by a set of regularly spaced samples, provided that the sampling frequency is greater than 2 x 'B'. This means that if you want to sample an audio signal whose highest frequency component lies at 20kHz, any sampling frequency higher than 40kHz is sufficient.
When Reeves patented his ideas, it wasn't possible to measure samples sufficiently quickly to record the full human auditory bandwidth, which is usually quoted as 20Hz to 20kHz. But, in 1947, the transistor was invented. Although too slow in its earliest incarnations, a quarter of a century of technological development increased the speeds of transistors to the point where digital audio devices became possible.
The first commercial digital recorder, Soundstream, appeared in 1975, and used two devices to create a recording: a PCM converter that sampled the input signal and then converted the resulting numbers into a video-type signal; and a video recorder with the bandwidth (greater than 1MHz) necessary to store the stream of data thus produced.
Why Wasn't It "Perfect Sound Forever"?
The first Soundstream recording was demonstrated in 1976, and by 1977 Sony and Philips had developed prototype digital recording, storage and replay systems. Did these sound any good? Not by modern standards, and I'm confident that carefully made 15ips or 30ips analogue recordings would have sounded better than these early systems, with more depth, greater accuracy, more 'air' and more 'warmth', whatever you take those words to mean in an audio context.
 2. Non-linearity in the analogue-to-digital converter.If we assume that the storage medium and replay mechanism of an early digital recorder was error free (which, because of cost considerations, is not a safe assumption), the reason that these systems sounded poor was not a deficiency in the Sampling Theorem or in the concepts of digital audio. Reeves had got it right nearly 50 years earlier — the audio deficiencies were a consequence of the audio converters available at the time. It was extremely difficult and expensive to build a good 16-bit, 44.1kHz converter in the 1970s, and not much easier in 1982, when CDs first appeared. Consequently, neither the A-D converters in studio equipment nor the D-A converters in consumer products were good enough to live up to the hype that accompanied the launch of digital audio.
2. Non-linearity in the analogue-to-digital converter.If we assume that the storage medium and replay mechanism of an early digital recorder was error free (which, because of cost considerations, is not a safe assumption), the reason that these systems sounded poor was not a deficiency in the Sampling Theorem or in the concepts of digital audio. Reeves had got it right nearly 50 years earlier — the audio deficiencies were a consequence of the audio converters available at the time. It was extremely difficult and expensive to build a good 16-bit, 44.1kHz converter in the 1970s, and not much easier in 1982, when CDs first appeared. Consequently, neither the A-D converters in studio equipment nor the D-A converters in consumer products were good enough to live up to the hype that accompanied the launch of digital audio.
There are three major areas in which real converters diverge significantly from the mathematical ideal.
Firstly, we have to consider the accuracy and linearity of the sampling circuits employed. Imagine that an analogue voltage of precisely 1.000000V results in a digital sample with a value expressed as a decimal of (for the sake of argument) 1,000,000. In the 1970s and 1980s it was extremely unlikely that a voltage of 2.000000V would then result in a sample with a value of 2,000,000. It might have been 2,000,001 or 1,999,999 or, more likely, would have exhibited a significantly larger error. Either way, this lack of 'linearity' resulted (and still results) in audio distortion. If the error is random (say, because of electronic noise in the circuitry) the result is audio noise, similar to that generated by analogue electronics, and it is probably not too disturbing. But if the error is systematic, there will be a consistent distortion, and this can result in unpleasant digital artifacts. This is shown very coarsely in diagram 2, above, in which a hypothetical analogue signal that is increasing in amplitude at a steady rate (so that a straight line exists for the duration covered by the four samples shown) is inaccurately sampled. The timing of the samples is correct, but one of them takes a value that is too low, while another takes a value that is too high. If an accurate D-A converter later converts these samples back into an analogue signal, the result is a distorted version of the input.
Secondly, we have to consider the accuracy of the clocks driving the converters. In the types of sampling systems used for digital audio, the gaps between samples should be absolutely consistent, both when recording and when replaying. Any deviation from the ideal is called 'jitter' and, again, this will result in distortion and noise. This is because some of the samples are being measured a little early or a little late, even if the average sample rate is consistent and correct.
 3. Jitter in the analogue-to-digital converter.
3. Jitter in the analogue-to-digital converter.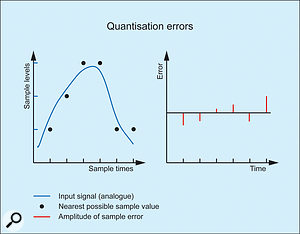 4. Quantisation errors.Even at the birth of digital audio the problems introduced by jitter were small, and considerations such as anti-aliasing (which we will address in a moment) were, and remain, more likely to degrade the sound. Nevertheless, let's illustrate the problem in the same way as we did for the non-linearity shown in diagram 2.
4. Quantisation errors.Even at the birth of digital audio the problems introduced by jitter were small, and considerations such as anti-aliasing (which we will address in a moment) were, and remain, more likely to degrade the sound. Nevertheless, let's illustrate the problem in the same way as we did for the non-linearity shown in diagram 2.
Consider a signal sampled at 44.1kHz, and imagine that the clock that determines when the samples are taken is accurate to one millionth of a second. This sounds very accurate, but if you do a little maths you find that any given sample might be taken as much as five percent too soon or too late. This would be a totally unacceptable error, and nowadays clocks are accurate to millionths of millionths of seconds, which is way beyond the technology available to the early systems.
Diagram 3 shows an exaggerated example of this. The second and third samples are accurate in the sense that they correctly represent the amplitude of the signal at the moment that that they are taken, but one has been measured too late, while the next had been measured too soon. This means that the values are not what they should be, and if they are then replayed through a DAC with a stable and accurate clock, the result, again, is distortion.
Thirdly, there's the resolution of the converter. Those of us who've watched digital technology progress through its 8-, 12-, and 16-bit stages know that the grainy textures generated by an Emulator 1 or a PPG2.2 can be superb synthesis tools but, at 'consumer' sample rates, such low-resolution systems are far from ideal for reproducing Mahler's Ninth wotsit.
Converting a changing analogue voltage to a stream of quantised values introduces errors that result in a maximum possible signal-to-noise ratio of approximately N x 6dB, where 'N' is the number of bits used in each sample. Unfortunately, this noise is only (relatively) benign if the recorded signal is itself random — in other words, noise. Real musical signals are not random, and the errors introduced are related to the signal (or 'correlated') in ways that lead to the introduction of some very unpleasant distortions.
Fortunately, this effect can be eliminated by adding a carefully chosen type of noise (known as 'dither') to the input signal. Add too little and the distortion remains, albeit at a lower level. Add too much and the resulting signal becomes unacceptably noisy. The mathematics regarding the ideal amount of dither (its power) and the nature of the noise used (its spectrum) is well understood, but the subject has nonetheless resulted in endless debate over the past 30 years, and it is still a contentious issue.
Toward 1-bit Converters
Before leaving behind the oversampling converter, it's worth noting that this also offers a significant benefit when considering the amount of noise introduced by quantisation. To cut a long story short, the total amount of noise added by the quantisation errors in diagram 4 is independent of the sample rate, but is always distributed over the total spectrum. Therefore, the amount of noise introduced into the audio band (20Hz to 20kHz) is 64 times less if you use a 64x oversampling converter and then filter the signal down to a bandwidth of 22.05kHz (the Nyquist frequency, remember) than it is if you sample directly at 44.1kHz. This increases the signal-to-noise ratio of a 16-bit converter from around 96dB to around 114dB, which is not a trivial improvement.
Interestingly, if we turn this idea on its head, we can begin to understand what a 1-bit converter is. If each additional bit in a sample improves its signal-to-noise ratio by 6dB, and each doubling of the sampling frequency improves the signal-to-noise ratio by 3dB, we can trade word-length for sample rate, and vice-versa. Consequently, 16 bits sampled at 44.1kHz are equivalent to 15 bits sampled at 4 x 44.1kHz (after low-pass filtering back to 44.1kHz), and to 14 bits sampled at 16 x 44.1kHz (after low-pass filtering back to 44.1kHz), and so on. The consequences of this are very far-reaching, but unfortunately they are also beyond the scope of this article.
Aliasing
Let's now conduct another thought-experiment, and imagine that we have a magical digital audio recording and replaying system that introduces no errors, and has impossibly high linearity, impossibly high resolution, and impossibly low jitter. We record some audio and the result still sounds horrible when we replay it. What the heck has gone wrong? Is digital audio still, in some way, inherently rubbish, or have we overlooked something important in the implementation of our imaginary system?
The clue to the identity of this 'something' is tucked away in the sampling theorem I mentioned earlier. It's the statement that the sampling frequency must be more than two times the highest frequency presented to the system. Please note, that's not "more than two times the highest frequency that you wish to record". It is two times the maximum frequency component in the signal presented to the A-D converter, and therein lies a very significant difference.
 5. A common way to represent aliasing.Consider a digital system that employs a sample rate of 40kHz. Half this rate (known as the Nyquist frequency) is 20kHz, so the Sampling Theorem says that any signal whose highest component lies below 20kHz can be sampled and later reconstructed perfectly (or, to be more precise, to the limits of accuracy of the system). But what happens if there are signal components that lie above 20kHz (even if you don't want to record them)? The answer is that these are 'reflected' off the Nyquist frequency and undesirable 'aliases' of them appear in the audio spectrum.
5. A common way to represent aliasing.Consider a digital system that employs a sample rate of 40kHz. Half this rate (known as the Nyquist frequency) is 20kHz, so the Sampling Theorem says that any signal whose highest component lies below 20kHz can be sampled and later reconstructed perfectly (or, to be more precise, to the limits of accuracy of the system). But what happens if there are signal components that lie above 20kHz (even if you don't want to record them)? The answer is that these are 'reflected' off the Nyquist frequency and undesirable 'aliases' of them appear in the audio spectrum.
By way of illustration, the static note represented by the harmonics in diagram 5, right, has four components lying above the Nyquist frequency, and these are reflected back at frequencies that would, upon reconstruction and playback, degrade the original sound. When this occurs during music, it creates very unpleasant audio artifacts. What's more, once alias frequencies have been introduced into a signal, they can (as a general rule) never be removed, so the degradation is permanent.
A better, but less common description of aliasing is shown in diagram 6, overleaf. When you look at the mathematics (don't worry, we won't...) you find that the action of sampling a signal creates multiple spectra, each with the same shape as the input signal spectrum, but reflected on either side of every integer multiple of the sampling frequency. This is quite a hard concept to express in words, but the diagram should make it clear, and also illustrates why we obtain the 'reflected' frequencies in diagram 5.
 6. A better representation of aliasing.
6. A better representation of aliasing. 7. Eliminating aliasing.Diagram 6 also tells us how to make aliasing go away. We simply need to create a gap between the input spectrum and the first alias (see diagram 7), and we do this by applying a low-pass filter to the input signal. In theory, you could use a very steep analogue filter to attenuate any unwanted high-frequency components sufficiently to ensure that the aliases lie below the resolution of the converter. However, if the highest wanted frequency is, say, 20kHz (as it is for high-quality music) and the sample rate is, say, 44.1kHz (as on a CD), the filter has to attenuate the signal by up to 96dB in about an eighth of an octave, which is a phenomenally steep slope, and wholly impractical in the analogue domain.
7. Eliminating aliasing.Diagram 6 also tells us how to make aliasing go away. We simply need to create a gap between the input spectrum and the first alias (see diagram 7), and we do this by applying a low-pass filter to the input signal. In theory, you could use a very steep analogue filter to attenuate any unwanted high-frequency components sufficiently to ensure that the aliases lie below the resolution of the converter. However, if the highest wanted frequency is, say, 20kHz (as it is for high-quality music) and the sample rate is, say, 44.1kHz (as on a CD), the filter has to attenuate the signal by up to 96dB in about an eighth of an octave, which is a phenomenally steep slope, and wholly impractical in the analogue domain.
Consequently, aliasing is removed in the digital domain using a device known as an Oversampling Converter. This samples the signal at a much higher sample rate than the range of human hearing demands, thus ensuring that any aliasing artifacts occur at supersonic frequencies. Consider a 64x oversampling converter: this has a Nyquist frequency of 1.411MHz so, given that no microphone can record frequencies anywhere near this high, we can use a very gentle analogue input filter, and reduce the frequency response to the required bandwidth using a steep, digital low-pass filter.
So why didn't the developers of the early digital audio systems use oversampling converters to minimise these problems? Simple... the technology didn't exist. As a result, many early digital recordings suffered from limited bandwidth (a loss of high frequencies), filtering artifacts, or aliasing itself. Again, there was nothing wrong with the theory, but the available hardware and software didn't allow the developers to implement it in anything approaching an ideal fashion.
Inadequate technology was also the reason why early digital audio editors sounded poor. This is because a word length suitable for capturing and replaying an audio signal may not be sufficient for manipulating it, so, while these systems could record, store and replay adequately, the moment they tried to do something as simple as change the gain or perform a cross-fade, the audio quality suffered. To understand this, imagine a situation where you want to decrease the loudness of a recording by dividing the value of each sample by a factor of two. Let's take two adjacent samples which start out with voltages of 10.0V and 11.54V and which, when sampled, take decimal values of "10.0" and "11.5" respectively (in this example, one decimal place is the highest resolution possible). The error in the second sample is 0.35 percent or thereabouts, but when the gain reduction is calculated, the error (a new value of 5.7 rather than 5.77) increases to 1.2 percent, which is very significant and would cause all manner of problems.
Of course, this is a hugely exaggerated example, but the principle holds in all digital systems, no matter how high the resolution. Therefore, to minimise the errors, modern systems use a large number of bits (typically 24) to sample and store each measurement, provide even more (usually 32, 40 or 64) in which to perform calculations, and use dithering to minimise artifacts when reducing the word length to write a new file or place the audio on, say, a CD. Again, this is technology that simply wasn't practical in the 1970s and 1980s, and its absence is yet another reason why older digital processors sound less accurate and are noisier than their modern descendents.
That's Not All
At this point, you may feel that you are getting a good grasp of the principles of digital audio, and maybe even the impression that all its problems can be overcome by designing accurate converters and specifying sample rates and word lengths that minimise the down sides of quantising a signal into discrete samples. But there are still many potential pitfalls. Here's an example...
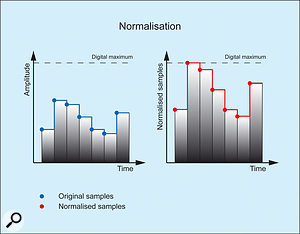 8. Normalising the samples in a digital audio recording.
8. Normalising the samples in a digital audio recording. 9. Normalisation leading to clipping.A few days ago, Martin Smith of Streetly Electronics (the Mellotron people) asked me why normalising an audio sample was introducing distortion in his older DAW. As you are probably aware, normalising (as applied in a modern context) is the operation of applying gain so that the maximum amplitude in each of a set of recordings is the maximum amplitude available to the system, with all the other samples scaled accordingly. I have shown this in diagram 8, below, which gives the common representation of a digital signal as a sequence of samples, and with each value 'held' before the next.
9. Normalisation leading to clipping.A few days ago, Martin Smith of Streetly Electronics (the Mellotron people) asked me why normalising an audio sample was introducing distortion in his older DAW. As you are probably aware, normalising (as applied in a modern context) is the operation of applying gain so that the maximum amplitude in each of a set of recordings is the maximum amplitude available to the system, with all the other samples scaled accordingly. I have shown this in diagram 8, below, which gives the common representation of a digital signal as a sequence of samples, and with each value 'held' before the next.
Now, perhaps the greatest myth in digital audio relates to the misconception that digital signals are shaped like staircases, and that much of their 'brittleness' is a consequence of the steps. This is nonsense. Digital signals are not shaped like anything — they are sequences of numbers. Unfortunately, the type of representation in diagram 8 has led many people to confuse graphics with reality.
Let's be clear. When the samples in a digital signal are converted back into an analogue signal, they pass through a device called a reconstruction filter. This is the process that makes the Sampling Theorem work in the real world. If there are enough samples and they are of sufficient resolution, the signal that emerges is not only smooth but virtually identical to the analogue signal from which the samples were originally derived. Of course, it's possible to design a poor reconstruction filter that introduces unwanted changes and artifacts but, again, this is an engineering consideration, not a deficiency in the concept itself.
Now let's return to the normalised signal in diagram 8, and consider diagram 9. This shows that reconstruction would require the maximum signal level value to exceed the limit of the system. Because it cannot, clipping distortion occurs and, yet again, digital audio sounds 'bad' when there is nothing wrong with the principle, only the implementation.
Where Now?
So there we have it. Even if we ignore the risk of errors in the storage and the replay of digital samples, the effects of non-linearity, jitter, an inadequate number of bits, aliasing and poor signal processing all contribute to signal degradation and to the audible problems exhibited by early digital systems. As a result, the myth entered the public consciousness that digital audio per se sounded bad in some systematic and irresolvable way. But if we accept the Sampling Theorem and embrace good engineering practices, there is no reason why today's digital audio systems should be anything other than superb ways to store, manipulate and replay audio. Using modern technology, developers can approach the ideals much more closely, so that, in the real world, digital audio is not by necessity any worse sounding than the best analogue equipment, and in many ways it can be superior. In truth, there are trade-offs in terms of noise, accuracy and flexibility with both the analogue and digital approaches, and the question "Which is better?" should probably be met with the disdainful response, "For what?".
Unfortunately, the current trend is away from high-quality consumer digital audio. Persuading the music industry to replace 44.1kHz equipment with 96kHz 'high definition' equivalents was hard enough in the 1990s, when there were high hopes for DVD-A and SACD. Trying, today, to get the tattered remains of the industry to replace perfectly serviceable 96kHz equipment with 192kHz or even DSD systems (so that they can make wonderful recordings for you to destroy by conversion to MP3) is significantly harder. So, in a perverse twist of fate, we now find ourselves back where we started in the 1970s, with high-quality analogue recordings often sounding more pleasant than the digital alternatives that many people choose to listen to... and that really is bollocks!
Thanks to Dr Christopher Hicks of Cambridge University for ensuring that this article leaves no digital egg on my (somewhat analogue) face.
