 Figure 1: If an erroneous sample is detected, it can be discarded and an approximation made to its value by interpolation from preceding and following samples. In practice, the resulting amplitude error is very small except when the signal consists of loud high frequencies.
Figure 1: If an erroneous sample is detected, it can be discarded and an approximation made to its value by interpolation from preceding and following samples. In practice, the resulting amplitude error is very small except when the signal consists of loud high frequencies.
PART 3: In the third instalment of our series on the techniques and technology of digital audio, Hugh Robjohns turns his attention to digital audio error detection and correction — and some of the problems associated with them! This is the last article in a six‑part series.
<!‑‑image‑>Last month, we concluded our examination of the basic operation of an analogue‑to‑digital converter with a look at the various problems and clever solutions associated with quantising. This month, we will consider what has to be done to protect the binary data generated by the A‑D from recording and transmission errors.
The first thing to appreciate is the sheer amount of data created every second by a stereo A‑D converter. Assuming for the moment a converter working at, say, 44.1kHz with a 16‑bit output, the total data generated every second is:
2 x 44,100 x 16 = 1,411,200 bits per second or 176,400 Kilobytes per second
So in one minute, there will be something like 10.5Mb of audio data to store and in one hour, 635Mb! If you scale it up for a 48kHz converter with 24‑bit resolution, an hour's worth of recording would require just over 1Gb of storage. That is a lot of data to have to look after — and as yet we have not given any thought to adding error protection data or any auxiliary subcodes for copyright status or timing information.
At present, there is great pressure within the recording industry to move up to digital systems running at a 24‑bit resolution and with a 96kHz sampling rate. In such systems, the amount of data stored during recording doubles — roughly 2Gb per hour for stereo, and 6Gb for six‑channel surround! This is the reason why the high‑resolution audio lobby are desperate to get the agreements sorted out over the audio‑only version of the Digital Versatile Disc (DVD) with its 4.7Gb (per layer) capacity — an ordinary CD can only store about six minutes or so of six‑channel high‑resolution audio!
Error Protection
 Figure 2: 'Even parity checking' on the rows and columns allows erroneous data to be detected and the position of the faulty bit identified. Since the data is binary, if a bit is known to be wrong, inverting it will correct the error.
Figure 2: 'Even parity checking' on the rows and columns allows erroneous data to be detected and the position of the faulty bit identified. Since the data is binary, if a bit is known to be wrong, inverting it will correct the error.
The data generated by an A‑D converter carries the quantised sample values of the original analogue audio and so any corruption to that data will result in erroneous sample values, and, ultimately, an incorrectly reconstructed waveform (which may appear distorted or 'clicky' to our ears). Clearly, any form of audible error is undesirable, and so steps must be taken to preserve the original data with an error protection system of some kind.
<!‑‑image‑>The error protection strategies used in digital audio systems are extremely complex and are optimised for a specific medium — the system employed by DAT differs from that used on CD, for example, because the nature of the predominant errors are different. However, all audio error protection systems follow the same basic strategies, which start with a mechanism for detecting the presence of corrupted data. After all, the best error correction system in the world is no good if it can't spot corrupted data in the first place!
The simplest way to spot corrupted data is to use a parity check — a very common system in use in everything from ISBN codes on books to barcodes on tins of soup! The idea is to add some extra information to the data which imposes a known property on the digital data. For example, in an 'even‑parity' system, a single data bit is added to the original data such that the total number of 1s is always an even number (the parity check bit is shown in brackets):
1011[1] and 1010[0]
Should one bit of the data (or parity check) become corrupt, the parity check will fail and the system will know that the data is not valid. This simple system can only detect a single bit in error — two corrupted bits will appear to provide a valid parity check and this demonstrates an important facet of all error detection systems, no matter how elaborate: firstly they have to burden the wanted data with additional bits (often called redundant data), and secondly, there will always come a point where the system fails to spot the errors.
Error detection systems are designed to be capable of detecting errors beyond the anticipated peak error rate of the medium concerned, and the amount of redundant data added to the audio data is never so great that storage times are adversely affected. In the case of the CD format, for example, roughly four bits have to be recorded for every three audio data bits which seems like a lot but in fact, employing a decent error detection/correction system actually allows more data to be stored on a given medium rather than less, because the data can be packed more densely. Although this will lead to more data becoming corrupted by flaws in the medium, the presence of the detection/correction system enables the data to be recovered accurately.
A commonly employed error detection system in digital audio applications is the Cyclic Redundancy Check Code (CRCC) which typically achieves an error detection success rate of better than 99.9985% — which is, to all intents and purposes, perfect! In fact, the CD specification claims to suffer fewer than one undetected error in every 750 hours of replay, in the worst case.
Concealment
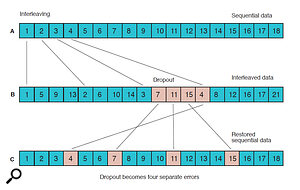 Figure 3: Interleaving data to avoid errors due to localised dropouts.
Figure 3: Interleaving data to avoid errors due to localised dropouts.
A simple system like parity checking can detect the presence of errors but can not correct them, because it has no way of identifying which bits are corrupt. In this situation, all that can be done is to discard the faulty data and try to guess at what the true value was, based on the preceding and following data — a process called Interpolation or Concealment. This process is never used in pure data applications (such as on the hard disk of your PC), and is usually a last‑ditch mechanism in digital audio systems (although the NICAM stereo television system relies on exactly this as its main error handling strategy!)
<!‑‑image‑>To give you an idea of the rarity of interpolation, the CD specification states that an interpolation should be required fewer than once every 10 hours of replay. However, when required, the interpolation system can actually accommodate 12,300 missing data bits, which equates to something like 10 milliseconds of audio and about 8mm of damaged disc surface.
Interpolation works tolerably well in audio systems because sample amplitudes generally change slowly and reasonably predictably from one sample to the next due to the majority of audio energy being concentrated in the low frequencies. Thus, averaging the preceding and following samples to approximate a missing one in the middle works surprisingly well and it is only with very loud high‑frequency signals that the interpolation process produces audible amplitude errors. Figure 1 shows how a erroneous sample is discarded and a new one interpolated, and also how large errors can arise when interpolating high‑frequency signals.
Correction
 Figure 4: In a Block Interleave system, data within the block is scrambled in a known sequence, but the data on the block boundaries always remains sequential, allowing edits or record drop‑ins to be made without upsetting the interleave structure.
Figure 4: In a Block Interleave system, data within the block is scrambled in a known sequence, but the data on the block boundaries always remains sequential, allowing edits or record drop‑ins to be made without upsetting the interleave structure.
Concealment is obviously not the ideal solution, and some means of correcting detected errors would be preferable. However, this relies on the detecting system being able to pinpoint the erroneous bits which implies some form of cross‑checking. As a simple example, consider a 16‑bit digital word arranged as four, four‑bit words in a 4x4 table, with even parity added to both the rows and columns (including a parity check on the parity bits!). Practical error correction systems are far more elaborate than this, but the concept remains valid.
<!‑‑image‑>In the example shown here, one of the bits has been corrupted and because it is now possible to cross‑check the parity on the rows and columns, the faulty bit can be identified. Again, this simple system can only correct a single corrupted bit. Two faulty bits will lead to the system being unable to identify their location, but at least the system still flags the entire word as invalid and so concealment could be employed.
Practical error correction systems are frighteningly complicated and go by names such as the Cross‑interleaved Reed‑Soloman Code (used on CDs) and the Double Reed‑Soloman Code (used on DAT). To give an indication of the power of these systems, the CIRC system on a CD can completely correct a block of 4000 missing bits, which equates to 2.5mm of unreadable data on the disc.
Interleaving
With any error protection system, if too many erroneous bits occur in the same sample, there is a risk of the error detection system failing, and in practice, most media failures (such as dropouts on tape or dirt on a CD), will result in a large chunk of data being lost, not just the odd data bit here and there. So a technique called interleaving is used to scatter data around the medium in such a way that if a large section is lost or damaged, when the data is reordered many smaller, manageable data losses are formed, which the detection and correction systems can hopefully deal with.
In Figure 3, the original sequential data (A) is scrambled in a known sequence (B). If a section is lost through, say, a tape dropout, then when the data is unscrambled (C), the large block of missing data which would defeat the error protection system becomes several small blocks which are retrievable.
...the interpolation system can actually accommodate 12,300 missing data bits...
Interleaving is a standard element in the error protection process, but it has a number of implications when it comes to digital editing and punching‑in or out of record. The problem is that because the data is not stored sequentially on the tape or disc, how can aprecise edit point be located? Imagine wanting to punch in after sample eight in the example above. On the tape, sample nine is actually stored some way before sample eight — and so whether you started recording new data after sample eight or before sample nine, the interleaving structure would be destroyed and no error correction system would be able to make any sense of it! The result would be a fairly major splat of the kind that most DAT machines make when you drop into record on pre‑recorded material!
One solution is to use a form of interleaving known as Block Interleave, a simple version of which I have used in Figure 4, above. The idea is that the data is grouped into blocks and although the data within each block is scrambled according to the interleave rules, the first and last sample always remain in their original positions so that at the block boundaries the data is always sequential, although only for those two adjacent samples. In the example here, the block interleaving is performed by loading the sequential data into a 'memory' on a row‑by‑row basis, but recording it in a column‑by‑column order. Thus, sample 16 and 17 will always be adjacent and a drop‑in could be made at this point without destroying the interleaving structure.
In fact, a block interleave system like this is used in DAT, but the block boundaries only occur once every 30 milliseconds, and although it is perfectly possible to design a DAT recorder to only enter or exit record at a block boundary, most don't bother, hence the inevitable clicks and splats! In any case, it could be argued that only being able to edit at 30‑millisecond intervals is not good enough — it equates to about 1cm of tape at 38cm per second (15ips) and most proficient tape editors could do a lot better than that! Fortunately, there are ways to overcome the problems of block interleaving which involve four‑head head drums and pre‑reading — something we will look at next month.
Coming Up...
In the next instalment of this series, I will describe some of the inner workings of the common digital tape formats, including DAT and the various multitrack formats.
Error Status
The kind of detection, correction and concealment systems used on current digital audio systems is, without exception, extremely powerful and it is only in cases of extreme provocation that problems become audible. For the consumer, this kind of serene perfection is one of the most desirable qualities of a digital audio system. However, for the professional it can be a real problem.
With analogue systems, quality deteriorated progressively — for example, if the tape heads became dirty, the gradual loss of high frequencies would hopefully be noticed by human ears before it became a serious problem. However, in a digital system that is no longer the case. Dirty heads on a DAT machine will cause an increasing error rate, but the error correction system will cope... until it really can't any longer, and has to interpolate. But even then, there is a good chance that you will be none the wiser until even the concealment system gives up and the output mutes in disgust!
Since you can no longer rely on your ears to detect problems in the replay transport or medium, digital systems really should incorporate some form of indicator of how hard the error correction and concealing systems are having to work, which will give a good idea of the state of the transport and the quality of the tape or disc.
All that is needed is a pair of lights, one to illuminate when an error has been corrected and the other to show when correction was impossible and an interpolation has occurred. The correction light would flash occasionally — the rate being dependent on the format, medium, and transport. After all, the error correction system is there for a good reason and you would expect it to earn its keep. However, the correction light flashing more frequently than normal could mean the medium is nearing the end of its useful life, or the transport is suffering in some way (such as dirty heads or opto‑sensor). At this stage, making a digital clone would preserve the original audio data by placing it onto a more robust medium. If the concealment light flashed more than very rarely it would be a good indication that real problems are lurking just under the surface and something needs to be done rather urgently to preserve the sonic integrity of the signal.
Virtually all the error protection chips used in CD players, DAT machines and digital multitracks provide the signals required to drive the kinds of indicator described here, but very few machines actually implement the feature. A few professional DAT machines offer the facility — the Sony 7000 and the Fostex D‑series DAT machines for example, and some of the Panasonic DATs provide a numerical log of corrected errors — but they are very much in the minority. Manufacturers are very reluctant to put big lights on the front of their 'perfect' machines which say Error or Interpolation (for obvious reasons), but it is something which we should be demanding as users. How else can we discern the condition of the machinery or the precious master tapes we record and replay on it?
