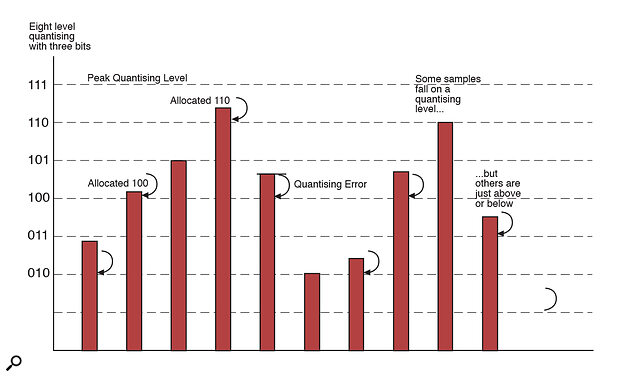
 Figure 1: A 3‑bit binary scale provides eight quantising levels. Some samples fall precisely on a level, but most miss by a small amount, and in this example, they would be allocated the binary value of the level immediately below their actual level. Thus the binary value does not reflect the true amplitude of the sample and the difference is called the quantising error.
Figure 1: A 3‑bit binary scale provides eight quantising levels. Some samples fall precisely on a level, but most miss by a small amount, and in this example, they would be allocated the binary value of the level immediately below their actual level. Thus the binary value does not reflect the true amplitude of the sample and the difference is called the quantising error.
Hugh Robjohns continues his look at the techniques and technology of digital audio. This month — quantising and oversampling.
Last month, we looked at the development of digital recording, and considered the sampling process — the first stage in turning an analogue signal into a digital one. This month we will examine the second stage, quantising, which is the conversion from a sampled analogue signal into a true digital one. We will also look at the theoretical and practical problems inherent in quantising, and some of the clever solutions that have been developed to overcome them.
<!‑‑image‑>We saw last month how the sampling process chops up an analogue audio signal into brief, discrete fragments — snapshots of how loud the audio is at precise moments in time (see the 'Previously On One Bit At A Time...' box for a brief recap of the main points of sampling). Essentially, quantising is where the amplitude of each sample is measured, giving a numerical value which can be stored or transmitted as pure digital data.
Quantising is inherently an imperfect process — there will always be some level of inaccuracy in determining the amplitude of a sample. The problem can be thought of in terms of measuring a room for a new carpet with a tape measure scaled only in whole metres. If the width of a room was found to be more than four metres but less than five, what figure would you choose? If you specify the width as four metres, when the carpet arrives it won't reach the edge of the room, but if you say five metres, it will extend halfway up the wall!
The solution, of course, is to use finer gradations on the ruler — if the room was measured to the nearest millimetre, there would be no discernible gaps or overlaps at all. In other words, the measurement errors would be significantly less and the carpet would fit perfectly.
Audible Errors
 Figure 2: As the signal becomes sufficiently small to only cross a few quantising levels, the quantising errors cease to be random, but become directly related to the audio signal, and are audible as distortion instead of noise. When the signal remains between two quantising levels, all samples take on the same amplitude and the audio signal is no longer represented at all.
Figure 2: As the signal becomes sufficiently small to only cross a few quantising levels, the quantising errors cease to be random, but become directly related to the audio signal, and are audible as distortion instead of noise. When the signal remains between two quantising levels, all samples take on the same amplitude and the audio signal is no longer represented at all.
When it comes to quantising the individual samples of an analogue audio signal, it turns out that our ears can easily hear very small errors in the measurements — even down to tiny errors as small as 90dB or more below the peak level — so we have to use a very accurate measurement scale. Figure 1 shows a few audio samples being measured against a very crude quantising scale simply to show the principles involved. Each level in the scale is denoted by a unique binary number — in this case, three bits are used to count eight levels (including the base line at zero).
Some samples will happen to be at exactly the same amplitude as a point on the measurement scale, but others will fall just above or below a division. The quantising process allocates each sample with a value from the scale, so sometimes the quantised value is slightly lower than the true size of the audio sample, and sometimes slightly bigger. These errors in the description of a sample's size are called quantising errors and they are an inherent inaccuracy of the process.
When the digital data representing the quantised amplitude values is used to reconstruct samples for replay, some of those samples will be generated slightly louder or quieter than the original analogue audio signal from which they were derived — they will not be entirely accurate. However, whether an audio sample falls on, above, or below a quantising level, and by how much a level is missed is essentially random — and a random signal is noise. Consequently, quantising errors tend to sound like hiss — white noise — added to the original audio signal.
The only way to make quantising noise quieter is to reduce the size of the quantising errors, and the only way that can be done is by making the quantising intervals smaller — in other words, by using a finer, more accurate scale for the measurements — just like in the carpet example earlier. The errors will still be there, but if you choose small enough quantising intervals, the errors become vanishingly small, as does the hiss. However, finer gradations require more quantising levels, and so more binary digits are needed to count them.
<!‑‑image‑>If the number of quantising levels is doubled, the spacing between individual levels must be halved, and so the potential size of quantising errors must be halved as well. A doubling or halving (in terms of dBs) is 6dB; so every time the number of quantising levels is doubled, the hiss caused by quantising errors is reduced by 6dB. In binary counting, each extra bit added to the number allows twice the number of levels to be counted — three bits can count eight quantising levels, four bits count sixteen, and five bits count 32 levels. This relationship gives us a handy rule of thumb to estimate the potential dynamic range of a digital system: For each extra bit used to count quantising levels, quantising noise is reduced by 6dB.
So, for example, an 8‑bit system should have a dynamic range of 48dB, a 16‑bit system (such as DAT and CD) should have a range of around 96dB, and a 24‑bit system about 144dB.
Quantising Distortions
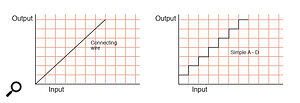 Figure 3: The transfer plot for a connecting wire is a straight line — what goes in comes out! A simple A‑D converter, however, has a characteristic staircase plot caused by the discrete nature of the quanstising levels.
Figure 3: The transfer plot for a connecting wire is a straight line — what goes in comes out! A simple A‑D converter, however, has a characteristic staircase plot caused by the discrete nature of the quanstising levels.
Quantising noise might seem relatively benign, but I have not told the whole story yet. Quantising errors only sound like white noise if the errors are distributed randomly — something which is true for large audio signals crossing lots of quantising levels. However, when a quiet signal is crossing only a few quantising levels the errors are directly related to the audio signal instead of being random, and so the errors become audible as gross distortion rather than a benign hiss (see Figure 2).
Furthermore, if the signal becomes sufficiently small that it remains between two adjacent levels, samples will be coded with the same value, and on replay, the reconstructed signal will be a steady (and completely silent) DC voltage!
What this means in practice is that a loud signal will sound slightly hissy (depending on the number of bits used to define quantising levels), but as the signal level falls, it will become more and more distorted until it finally breaks up before disappearing completely; hardly the kind of thing you'd want associated with a high‑quality audio system. Nevertheless, this problem was very common in the first few generations of digital recorders. The break‑up effect is most noticeable on reverb tails and the general background acoustic tended to be rather 'granular' and gritty.
...dither is an essential aspect of the conversion process, just like bias in a tape recorder
All Of A Dither
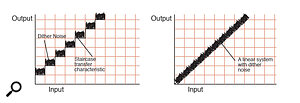 Figure 4: Adding the dither noise effectively 'blurs' the staircase plot (left) so that a straight line can be assumed — the recording system has become linear. However, the system also now has a fixed noise floor equivalent to one quantising level (right).
Figure 4: Adding the dither noise effectively 'blurs' the staircase plot (left) so that a straight line can be assumed — the recording system has become linear. However, the system also now has a fixed noise floor equivalent to one quantising level (right).
A good way to think about this problem, and how to cure it, is to consider something called a transfer plot — a graph which relates input signal level to output signal level (see Figure 3). As an example, an interconnecting cable will pass any level changes on its input directly through to its output perfectly linearly, so the plot shows a straight line at 45 degrees. However, a digital system is far from linear — as the input signal increases in level, the output remains fixed at a quantising level before suddenly jumping to the next level. Consequently, the transfer curve looks like a staircase instead of a desirably straight line.
Analogue tape recording suffers a similar non‑linearity problem because the properties of magnetic tape are far from perfect. However, in this case, the problem is overcome by employing an inaudible, very high‑frequency signal (called bias) which makes the magnetic properties behave more linearly. Digital audio systems have to resort to a similar tactic to create a linear transfer characteristic using an audible signal called dither.
Dither is essentially a very small amount of white noise (equivalent in amplitude to one quantising level — about 90dB below peak level in a 16‑bit system) which is deliberately added to the analogue audio signal as it enters the A‑D converter. Thinking back to the transfer plot, this dither noise effectively 'fills in' the steps in the transfer curve so that a straight line can be drawn through the noisy staircase. When correctly dithered in this way, the digital system behaves perfectly linearly, but there is a small amount of noise always present — the amplitude of which rises and falls as the input signal increases in level through each quantising band (see Figure 4).
<!‑‑image‑>As the input signal gets quieter, it no longer becomes increasingly distorted, but remains perfectly accurate and clean, even as it fades below the smooth background hiss — behaving just as an analogue system would. Dither is a very complex subject which is actually bound up with statistical distributions. Consequently, the different varieties of dither are referred to in terms of statistics. The most commonly used version is known as TDDF (triangular distribution dither function), although a number of others are used on occasion.
<!‑‑image‑>Dither is not normally something which is adjustable in an A‑D converter — the manufacturer sets the appropriate level of dither when the unit is designed. However, the important point to remember is that dither is an essential aspect of the conversion process, just like bias in a tape recorder. However, dither also plays a vital role when digital word lengths are altered, for example in reducing a 20‑bit master recording for release on a 16‑bit format such as CD. This is an area where the user is able to alter the type and amount of dither used (something I will return to in a later article).
The only critical aspect of dither is its statistical properties, and it is common for the frequency response of the dither signal to be tailored (without altering the statistics) to complement the natural sensitivity variations of the human hearing system. By reducing the amplitude of the dither signal in the middle frequencies, and boosting it in the very low and very high regions, the averaged level of the dither signal remains the same, but it is far less audible in the middle frequencies, where our hearing system is most acute. Thus the perceived noise floor is lower than it would otherwise have been. This is how some manufacturers claim to produce 16‑bit systems which sound as quiet as 20 bit systems, even though they have a measured performance which is identical to any other 16‑bit system!
Overloads
 Figure 5: With oversampling, a very gentle analogue anti‑alias filter is used, and a digital linear‑phase brickwall filter is then applied at 22.05kHz. The data stream is also resampled to the desired 44.1kHz sample rate during the digital filtering process.
Figure 5: With oversampling, a very gentle analogue anti‑alias filter is used, and a digital linear‑phase brickwall filter is then applied at 22.05kHz. The data stream is also resampled to the desired 44.1kHz sample rate during the digital filtering process.
So much for what happens at the bottom end of the quantising scale, but what happens when the analogue input signal is so large it exceeds the available measurement scale? Once the original audio signal goes beyond the top quantising level, the only thing the quantiser can do is allocate each sample with the maximum count until it falls back within range again. When the digital signal is later reconstructed to an analogue output, all the samples which exceeded the range will have the same (maximum) size. If the original waveform was sinusoidal, it will have become 'clipped'.
In the analogue world, clipping can sound perfectly acceptable — indeed, it is a technique often used to create distorted guitar effects. Severe clipping tends to make any audio signal look like square waves, so although a pure sinusoid signal contains only one frequency, when it is clipped to resemble a square wave, it will acquire a wide range of odd harmonics — a clipped 10kHz sine wave will have frequency components at 30kHz, 50kHz, 70kHz and so on — none of which are likely to be audible in a properly engineered analogue system. However, in a digital system, clipping caused by the quantiser running out of levels causes horrendous problems!
The odd harmonics created in a clipped digital signal extend far beyond half the sampling frequency, and because they are generated in the quantiser, after the anti‑alias filter, they inevitably cause severe aliasing. It is this aliasing which makes digital overloads sound so obvious and unpleasant, especially on any kind of audio material which has recognisable harmonic structures such as voices or acoustic instruments.
If you have made recordings on a digital format you may have discovered that it is possible to get away with brief digital overloads on certain types of material. Any sound which does not have a distinct harmonic structure is not adversely affected by aliased components after clipping. Perhaps the two most obvious examples are cymbals and snare drums — both of which are essentially composed of noise (albeit with a characteristic frequency spectrum). Aliased noise is just more noise, so brief clipping on snare drum transients or cymbal crashes will almost certainly go unnoticed — the worst that is likely to be audible is a subtle change in the tonal character of the relevant instrument, but only during the brief moment of clipping!
In terms of the theory, that is pretty much it for quantising. The more bits available to describe individual quantising levels, the smaller the intervals can be and the lower the inherent quantising noise (by 6dB for every additional bit used). Dither is essential to linearise the whole quantisation process, and a working headroom must be created to cope with overloads because the clipping causes aliasing, which sounds very unpleasant indeed.
Problems And Solutions
 Figure 6: The diagram on the left shows the relationship between quantising noise and peak audio level for a 1‑bit system operating at 44.1kHz. The diagram on the right shows how that noise floor is reduced by oversampling (by a factor of 64 in this case), and then how noise‑shaping reduces the noise in the wanted audio band even further.
Figure 6: The diagram on the left shows the relationship between quantising noise and peak audio level for a 1‑bit system operating at 44.1kHz. The diagram on the right shows how that noise floor is reduced by oversampling (by a factor of 64 in this case), and then how noise‑shaping reduces the noise in the wanted audio band even further.
There are a number of practical problems involved in making high‑quality analogue‑to‑digital converters. We saw last month how the anti‑alias filters are difficult to make, use expensive components, and tend to sound unpleasant because they have to have such steep rolloff curves. There are additional problems with the quantisation stage, because it is hard enough to ensure the 65,536 quantising levels of a 16‑bit system are uniformly spaced, let alone trying to do the same with the 1,048,576 levels of a 20‑bit system, or over 16 million in a 24‑bit system! Another problem is that the amplitude of an analogue audio sample decays slightly as the quantiser is trying to find out which level to label it with; this can affect the linearity of the measurement quite badly.
However, clever new techniques have been developed in recent years to overcome all these problems, and the most common approach these days is a converter technology called delta‑sigma modulation. Fundamentally, sophisticated digital techniques — number‑crunching, if you like — are used to replace the expensive and troublesome analogue circuitry wherever possible. Although expensive to develop, digital chips are very cheap to manufacture, so as well as solving most of the practical problems of the early converters, the new approach also improves profit margins!
The problem with the anti‑alias filter (and reconstruction filter for that matter), is that they have to have an incredibly steep rolloff to allow the audio band through but stop anything above half the sampling rate. Such filter designs tend to 'ring', which means they smear signals over time. In the early days, this was not thought to matter very much as long as the frequency response was flat, but we now know that such ringing does affect the perceived audio quality — particularly in terms of stereo imagingand naturalness. The only solution is to use much more gentle filter slopes, but that would require the sampling rate to be very much higher than it strictly needs to be, and CDs would then only have sufficient data capacity for 10 or 20 minutes instead of more than an hour.
...decimation... effectively takes the extra information obtained from oversampling the signal and turns it into increased bit‑resolution
Fortunately, there is another solution in the form of digital filtering. If the audio is sampled at a much higher rate than normal — say 64 or 128 times higher than 44.1kHz (a process called oversampling) — a very gentle analogue anti‑alias filter could be used with all the associated sonic and cost advantages (see Figure 5). However, it would not be possible to record the oversampled audio stream directly, so a mathematically complex, but cheap digital filter is used to create the necessary 'brickwall' cut‑off at 22.05kHz. By applying this filtering in the digital domain, it is possible to realise a perfect 'linear‑phase' filter which cannot exist in the analogue world. Part of this same digital filtering involves a process called decimation which is where the digital signal is resampled (still in the digital domain) to produce an output stream at the required sample rate of 44.1kHz. The decimation process doesn't just ignore the samples it doesn't need when creating a data stream at 44.1kHz; instead, it effectively takes the extra information obtained from oversampling the signal and turns it into increased bit‑resolution. So to achieve a certain signal‑to‑noise performance, a quantiser would have to operate with, say, 20 bits at 44.1kHz, but oversampled at 2.8224MHz (64 times higher) it may only require three or four bits, assuming the decimation process is performed accurately. This is another very important advantage of the oversampling approach.
<!‑‑image‑>The Delta‑Sigma Modulator takes this idea one stage further by only using one bit to measure the audio signal, but with a very high sampling rate. The one‑bit conversion determines whether each new sample is bigger or smaller than the preceding one — no more than that. Because the process is only 1‑bit, all the problems of creating thousands or millions of linearly spaced quantising levels is avoided and, because the system operates so fast, there is no time for the sample voltage to droop while the converter works out its amplitude!
<!‑‑image‑>Of course, a 1‑bit signal will have a huge amount of quantising noise, but this is dispersed across the entire and very wide oversampled bandwidth, whereas the wanted audio signal only occupies a small portion of that bandwidth (see Figure 6). Oversampling by a factor of two spreads the quantising noise over twice the bandwidth, and the noise power in the wanted audio band is reduced by 3dB. Oversampling alone is not sufficient to provide the kind of noise performance required in a professional system, so noise‑shaping is employed to reallocate the quantising noise within the spectrum (once again, see Figure 6).
Noise‑shaping is another digital filtering operation. The idea is to equalise the quantising noise so that it is reduced in the wanted audio band and boosted in the frequency spectrum above (the total noise power across the entire spectrum remains the same). When the digital anti‑alias filtering is applied, the audio band is retained and resampled at the required rate, and the unwanted quantising noise in the spectrum above the audio band is discarded. When correctly engineered, the overall performance of a delta‑sigma converter is typically better than any conventional A‑D converter, and it is the only practical technology which allows a 24‑bit resolution to be achieved.
Coming Up...
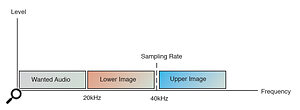 Here, the audio images are neatly separated from the wanted audio by ensuring that the highest frequency in the wanted audio is no higher than half the sample rate.
Here, the audio images are neatly separated from the wanted audio by ensuring that the highest frequency in the wanted audio is no higher than half the sample rate.
Next month, we will take a look at what has to happen to digital data before it can be recorded, and how some of the most common recording formats work.
Previously On One Bit At A Time...
<!‑‑image‑>Typically, digital audio systems sample audio at 44,100 or 48,000 times every second, although there are many other 'standard' sample rates. The regularity and stability of the timing in the sampling process is absolutely crucial to the ultimate quality of the digital audio system — timing inaccuracies introduced here cannot be removed later, and will result in unstable stereo imaging and increased noise.
The Nyquist Theorem states that the sampling rate must be at least twice the highest audio frequency being sampled. Consequently, the highest audio frequency a digital system is required to encode must be specified, and nothing above this frequency can be allowed to enter the system. This is achieved with an anti‑aliasing filter which would typically have a cutoff slope in the order of 200dB/octave. Early analogue filter designs were extremely expensive to manufacture, prone to drift, and tended to sound dreadful!
The sampling process chops up the analogue audio signal ready for quantisation, as discussed in this article. However, the process is actually a form of modulation where the audio signal modulates the amplitude of the individual samples. Any modulation process produces images of the original audio at the sum and difference frequencies — in this case between the audio signal and the sampling rate — and although these images are a side‑effect of the process and serve no practical purpose, they do have significant implications.
The diagram below shows a pair of images either side of the sampling rate. It is the lower image that causes all the problems, because it is very close to the original audio signal (hence the rule about the sampling rate needing to be at least twice as high as the highest audio signal to ensure a small separation). If audio signals above half the sampling rate are allowed into the sampling system, the lower image will extend downwards and overlap the audio band. This creates aliasing which is unmusical interference that can not be removed from the wanted audio.
Digital Headroom & Metering
In the analogue recording world, we are used to the idea that there is a nominal working level — say 0VU or +4dBu — but that it is permissible for signals to exceed this level by a certain amount called the headroom. On an analogue tape recorder, for example, the signal level can be increased well beyond the nominal line‑up level and although it will become increasingly distorted as the tape begins to saturate, it will probably remain acceptable (even desirable in some cases).
Digital systems have no headroom as such — the quantising levels are evenly spaced from the first to the last, and then they stop. Consequently, a suitable amount of headroom has to be created by defining and aligning the system such that the nominal operating level is some way below the maximum peak level. This allows the analogue metering on a sound desk, for example, to be related in some meaningful way to the recording level on the digital recorder.
The problem is in choosing a nominal digital operating level which equates to the universal analogue operating level of +4dBu (0VU). The critical aspect of metering for a digital recording is the true peak level of even the briefest transients. Unfortunately, VU meters only read average signal levels, and even analogue Peak Programme Meters (PPMs) tend not to respond to the fastest transients (this is quite deliberate, and is to avoid under‑recording, since brief transient overloads are inaudible on analogue systems).
Various standards have been published for digital operating levels. The early pseudo‑video digital recorders mentioned last month adopted ‑15dBFS (15dB below full‑scale) to equate with +4dBu (or 0VU). The European Broadcasting Union have specified a very similar standard of ‑18dBFS to equate to 0dBu (ie. ‑14dBFS aligns with +4dBu). In America they tend to use ‑20dBFS. All these standards assume you are working with a 16‑bit format making original recordings where there is a high degree of unpredictability in the absolute signal levels.
If the audio material has been carefully controlled (perhaps following post‑production and with sophisticated dynamics processing), a smaller headroom margin can safely be used — typically ‑10dBFS or even less. Ultimately, when the absolute peak level of the audio material is known, commercially released material is mastered to peak to 0dBFS (ie. there will be no headroom at all). Some recording engineers extend the headroom margin when working with converters which have greater resolution than 16 bits, since the available dynamic range is wider. Personally, I feel that there is more to gain from having a lower noise floor, so I stick with the standard 15 or 20dB of headroom when working with 20‑ or 24‑bitsystems. Digital clipping should be avoided wherever possible, and to help in that task most digital meters have expanded scales towards the peak levels. All digital meters also have an overload light for each channel, but some allow these to be configured to illuminate only after a certain number of consecutive peak value samples.
It is normal practice to peak a digital signal as high as possible — ideally just hitting the maximum quantising level on the loudest part of the audio material. In this case, a peak‑level signal is not an overload at all, so it might be misleading to see the overload light illuminate. However, a very loud high‑frequency signal, say at around 15kHz, might only be captured on three or four samples over a complete cycle, and probably only one of those would exceed the peak quantising level. In this situation, the overload light has to be illuminated on the one sample that hits peak level simply because it represents a genuine overload. The reality, of course, is that there is usually little energy at high frequencies in most audio material, and overloads in middle and low frequencies would involve large numbers of consecutive peak level samples.
Thus, overload indication is a complex problem and a common compromise is to only illuminate the overload light after three or four consecutive peak value samples (a standard set with the original CD mastering recorders). Thus it will not be erroneously triggered by legitimate peak‑level signals, but will show genuine middle‑ and low‑frequency overloads (although only extremely large high‑frequency overloads will register).
Personally, I prefer overload lights to illuminate with a single peak value sample because if I'm intentionally trying to just hit the top level (perhaps during post‑production or mastering), it is nice to know I have achieved my aim, and if I'm recording I need to know that I have hit the end stops — no matter how briefly!
How Many Bits Do We Need?
This is a good question for which there is no single correct answer, because it all depends on what the digital system is being used for. Domestic telephones, for example, use an 8‑bit system quite happily without noise being considered a problem, but no one would enjoy listening to an 8‑bit CD player for long! The 16‑bit specification for CD came about for two reasons. Firstly, when CD players were launched, 16‑bit converters were the absolute state‑of‑the‑art — it was not possible to do any better at the time. Secondly, around 90dB of dynamic range was thought to be more than enough in a domestic listening environment. A 16‑bit system counts 65,536 quantising levels, after all!
However, there are good arguments for professional recordings to be made with greater resolution than the eventual release format — for example, to allow post‑production to be performed on the material without compromising the quality of the final product. This is why 20‑ and 24‑bit systems are becoming increasingly common (together with the fact that the technology has become far more affordable). The potential dynamic range of a 24‑bit system is substantially greater than that of our own hearing, so that is considered to be the ultimate resolution required in a recording medium (although signal processing typically requires at least 32 bits, and often 56 or more, to ensure that calculation errors do not adversely affect audio quality).
