Synth School: Part 8

Paul Wiffen continues to examine transitional synthesis, covering the Wave Sequencing facility, first introduced on the innovative Korg Wavestation, and concluding with Emu's Z‑plane technique, which may be regarded as bridging the gap between S&S and today's physical modelling.

In the previous part of this series (see SOS April 1998), I began to talk about what I've termed 'transitional' synthesis methods, where, broadly speaking, a sound begins with a given harmonic content and evolves, to end with a different harmonic spectrum. This type of synthesis was exemplified, in different forms, by the Fairlight CMI, the PPG Wave series, the Sequential Circuits Prophet VS, and the Yamaha SY22, which was designed by the Sequential team for Yamaha after Sequential's demise. At the end of our last exciting episode, the ex‑Sequential personnel had parted company with Yamaha and had been taken under Korg's wing instead, where they continued to develop their concepts further.

Crossfade To Wave Sequencing

The transition from waveform to waveform in Sequential's Vector Synthesis, first seen on the Prophet VS, was a simple crossfade, and although two of these crossfades could be controlled or programmed by the joystick which was so integral to the Vector Sythesis system, the maximum number of waveforms which could be involved in a single sound was four. However, the San José‑based team's next development — termed Wave Sequencing — allowed up to 255 different waves to be involved. This innovation was introduced on the Korg Wavestation, which still featured joystick‑controlled Vector Synthesis, but added the much greater potential for transitional synthesis that wave sequencing gives.

Korg Wavestation.The closest precursor of wave sequencing was the PPG system of wavetable synthesis, where related single‑cycle waveforms were stored in a group of 32. The user could pick a starting waveform and then use an envelope or LFO to move around in the wavetable, causing timbral changes as the waveform being read out changed. Differences between adjoining waveforms were fairly slight, so the degree of timbral change was determined by how far and how fast the readout moved from the original starting point.

In the case of wave sequencing, coming 10 years after wavetable synthesis, there was much less economic restriction on memory for storing waveforms. As a result, instead of access being limited to 32 single‑cycle waveforms, full PCM samples were available, and up to 255 could be 'on‑line' for use by an oscillator in a sound. Each stage in the wave sequence could be occupied by a PCM sound radically different from the one before or after it in the sequence. The potential for striking sonic change is therefore much greater in wave sequencing, especially since the PCM waveforms can be deliberately moved around by the user to contrast as much as possible with their neighbours.

Not only can the number of steps in the wave sequence be up to 255, but at each step the user is also able to determine not only the PCM or single‑cycle waveform that is to be played, but also the duration of that wave and of the crossfade to the next wave. As a result, a greater degree of fine‑tuning is possible than in any preceding form of transitional synthesis. Of course, this also means that it can take a great deal of time to create a really complex wave sequence.

Figure 1: A 7‑step wave sequence, as shown in all Korg Wavestation manuals.To get a better idea of exactly how wave sequencing works, let's take a look at Figure 1, which is the diagram Korg supplied in all their Wavestation manuals, depicting a 7‑step wave sequence. It shows how each of the steps can have an entirely different waveform asssigned to it. Some are clearly PCM samples, such as Step 1 and Step 6, some are standard analogue waveshapes, such as Step 2 and 4, and others are more complex singlecycle waveforms, such as Step 7.

When the wave that each of these steps uses has been set, the level (volume) of each step can be individually set, as can the semitone (+/‑ 24) and fine (+/‑100 cents) tuning for each. In the diagram you'll see that Step 2's level is set louder than the others, and that Steps 4, 6 and 7 are quieter. The duration of each step is set as an arbitrary value between 1 and 499 or to Gate (which means that it lasts for as long as the key is held down). If the scale between 1 and 499 is not right for your needs, there's a neat little utility which lets you compress or expand the overall timescale of the sequence by up to 200%. This means that you can instantly make the wave sequence last twice as long or a fraction of its former length.

The transition between each step and the next is set by a crossfade parameter with another arbitrary value range, of 0 (no crossfade) to 998. This allows the timbral change between one step and the next to be instantaneous or to occur smoothly over whatever time interval you choose. This is the real power of wave sequencing — that these timbral changes can be as sudden or as gradual as you like.

Having set up some really interesting shifts of timbre, you may want to have them repeat. The Wavestation allows you to cycle around as many steps of the wave sequence as you want, in either a forwards or forwards/backwards loop. The number of repeats can be set from 1‑126, or you can specify infinite repeat, until the amplifier envelope fades the volume down completely.

The cycling of the steps still does not exhaust the possibilities of wave sequencing. Once the wave sequence is set, complete with crossfades and loop if required, the point at which playback of the wave sequence starts can be controlled by a variety of modulation sources. These include velocity, which can be set up so that harder keystrokes start playback from early in the wave sequence and gentler ones later on. This technique can be used with wave sequences which include harsher, brighter waveforms in the early steps and softer timbres in the later ones, to create a natural increase in harmonic content on faster keystrikes and a gentler sound on a lighter stroke. Alternatively, you can set a dynamic modulation source like mod wheel or aftertouch to change the step number of the wave sequence. In this case a start step is specified and this stage of the wave sequence is held until the modulation source is activated. Then the movement within the wave sequence is controlled by the mod wheel or aftertouch, so that timbral changes can be introduced as a real‑time expression factor. It is this type of facility which makes wave sequencing such a powerful form of synthesis, especially for lead synthesizer work.

More Fun In The Waves

Wave sequencing is only one of the techniques available on the Wavestation synthesizers. The instrument can be reduced to the simplest of analogue‑style architecture, with just one or two oscillators playing back single‑cycle waveforms through standard subtractive synthesis filters, but complete with specialist analogue techniques like Hard Sync (for those who remember back to our second instalment of Synth School). However, the number of oscillators can be set to four, and then they can be mixed, either in the normal way, or by using Vector Synthesis via a live joystick or the Mix Envelope, which stores this two‑dimensional mix as an envelope over time. Add to this the fact that any or all of the four oscillators can be set to play back wave sequences with their own filters and envelopes and you can see how complex each Patch can become (if the programmer has the time to set it all up). And since the Wavestation is multitimbral, it's possible to combine up to eight Patches into a Performance or 16 Patches on different MIDI channels in a Multi. At Patch, Performance or Multi level, the entire sonic result is passed through two effects, which are as good as those available on any synthesizer at the time (indeed, the effects were considered so good that the later, rackmount, Wavestation AD allowed external sound sources to be processed through them).

Although the sales of the Wavestation series of synths (including the much cheaper 1U Wavestation SR) never challenged the success of straight PCM‑based machines such as the Korg M1 or its successors, many people now declare the Wavestation to be their favourite Korg synth, or even their favourite synth of all time. It certainly has the potential to be an inexhaustible source of inspiration for real synthesis aficionados, allowing access to traditional subtractive synthesis, vector synthesis and wave sequencing. Not surprisingly, all three members of the Wavestation family hold their value extremely well on the second‑hand market, but if you can find one within your budget, it's a machine whose potential you are unlikely ever to exhaust.

Leading On A Z‑Plane

Figure 2: An example of an Emu Morpheus filter configuration.The next type of synthesis I'll be looking at, Z‑plane synthesis from Emu Systems, fits broadly into the category of transitional synthesis. However, the transition does not happen between different oscillator waveforms but in the filter section of the synth. Z‑plane synthesis was first implemented in the wittily‑named Morpheus (the name has nothing to do with the figure from Greek mythology but refers to 'morphing', a term which means to change from one thing to another), and its use of interpolation between two filter shapes is very reminiscent of how the Fairlight 'merged' from one waveform to another. Extremely complex filter shapes are created through the use of up to eight filter components, each of which is comparable to the traditional low‑pass, band‑pass or high‑pass filters or parametric equaliser bands (see Figure 2 for one configuration example). The resulting sculpting of the sound is far more precise and subtle than in any previous type of synthesis. In addition to the basic function of the filter, starting by removing the high and/or low end, peaks and notches can be placed at will anywhere across the entire audible frequency range.

Figure 3: The Morpheus filter can change its function over time, as this graph from the original Morpheus manual shows. Here filter characteristic A morphs into Filter characteristic B over time (the axis labelled 'Morph' here).Once you've managed to get your head round this, brace yourself, because we still haven't scratched the surface of Z‑plane synthesis. In fact, the basic Morph parameter on its own might be thought of as X‑axis synthesis. Another parameter, Frequency Tracking, introduces the equivalent of a Y‑axis into the equation. This is the closest parameter to the conventional filter cutoff, in that it moves the complex Morph filter up and down the frequency range (Figure 3).

In combination with the Morph parameter, Frequency Tracking gives two‑dimensional control over the filter shape (as illustrated in Figure 4). Unlike a conventional filter cutoff, though, the Frequency Tracking parameter cannot be moved in real time, but must be set at Note On (presumably because there has to be some limit on the processing power required). This makes it suitable for hooking to parameters like keyboard tracking and velocity, but unavailable for controlling from aftertouch or envelopes. However, the real‑time Morph parameter allows much more radical effects than filter cutoff movement, and thus more than makes up for the fact that you have to fix the Frequency Tracking at Note On.

Amazing Transformations

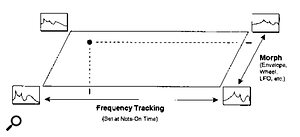Figure 4: Two‑dimensional control over filter shape is provided by the combination of the Morph parameter and the Frequency Tracking parameter.

The observant amongst you will have spotted that I've still not mentioned the 'Z' axis that completes Z‑plane synthesis: a third parameter, Transform 2. The function of this varies from Z‑plane filter to Z‑plane filter, but one example of what it can do is increase the size of the peaks and notches in the filter contour (similar to the individual peak which is increased in a conventional filter by the resonance control). Now we've introduced the Z‑plane into the equation, and now the three‑dimensional variations possible in the resulting filter contour are best visualised as the cube shown in Figure 5 (above), rather than the square in Figure 4.

The Transform 2 parameter, like the Frequency Tracking parameter, is also fixed at Note On, but this actually gives you more flexibility than most traditional filtering, where there is rarely any automatic control of resonance at all and you have to make do with the fixed setting whatever the note played or its velocity.

Figure 5: The Transform 2 parameter introduces the Z‑plane into Z‑plane synthesis, giving three‑dimensional variations in filter contour. The concept is shown here as a cube.Figure 5 shows the result when velocity is used to set Transform 2 and keyboard position used to set Frequency Tracking. Not all of the 197 filter types in the original Morpheus feature this third Transform 2 parameter, but about half do (so technically there are around 100 Z‑plane filter configurations in Morpheus). All the filter configurations are individually described in the manual, complete with comments and suggestions for specific uses, so there's no danger that you'll be left to yourself to try and work out where to use them (although I find that random assignment leads to some of the most exciting results — but then I've always been a great believer in serendipity, or the 'happy accident', ever since Jon Pertwee explained what it meant in an episode of Doctor Who!).

You really can make some major timbral alterations to your source waveform, changing it almost beyond recognition. In fact, the sheer range of filter types and the way they can be altered in performance, the technology used to create and modify the filter contours on an individual basis, and the resulting sonic variations in the sound, make Z‑plane synthesis a real precursor to last year's buzz technology, physical modelling (also known as virtual synthesis or acoustic modelling). This uses shedloads of DSP power to modify source waveforms in the same way that the physical modifiers of the real instrument (shape and size of resonating case or vibration column, for example) affect the input sound. Many of the Morpheus' filters are described in these terms — for example, F097 ("designed to make possible a set of piano presets that sound like they were recorded with the sustain pedal down"), or F105 ("designed to emulate some of the resonant characteristics of an acoustic guitar body"). As such, the Morpheus probably represents the missing link between instruments which just use DSP to add some effects sparkle, and those which create the entire sound through raw DSP, as in physical modelling instruments such as the Yamaha VL series or the Korg Prophecy or Z1.

Of course, we haven't really looked yet at the source waveforms that Morpheus allows you to filter in this radical way. Although the standard analogue waveforms we know and love from the very first Synth School (sawtooth, square and pulse in various widths) are available, these are crammed in with 48 sampled sounds, 22 harmonic waveforms (built additive synthesis‑style), 92 singlecycle samples from organs and synths, and 68 percussion sounds. So while Morpheus has something in common with PCM‑based synthesis, it also adds elements of analogue, additive and other types of synthesis along the way. If you're looking for a synth that will yield hours of experimentation and sonic creativity, Morpheus is a monster, but like so many of the best synths ever made, don't look to it for piano, strings, brass and drums (unless you like these with a twisted edge).

The real power of wave sequencing is that timbral changes can be as sudden or as gradual as you like.

Physical Relationship

With Z‑plane synthesis, we've started to touch on the technology used in physical modelling, which brings us up to date, as this is currently where all the big strides in synthesis are being made. From purely analogue models (those on the Roland JP8000 or Clavia Nord Lead, for example) through those which are based on other synthesis styles (such as FM on the Yamaha AN1x or other electronic instruments such as organs and electric pianos on the Korg Z1), to models of purely acoustic instruments (such as brass and woodwind from the Yamaha VL series, or plucked and bowed strings on the Z1), physical modelling is playing a greater and greater part in sound production on modern synthesizers. And it will become more and more prevalent as DSP gets more powerful and cheaper to implement.

Next time, we'll look at how physical modelling can not only imitate but sometimes go beyond the type of synthesis from which it draws its inspiration, to create even more exciting possibilities for those who are constantly searching for that something extra from a synth.